[자료구조] 단순 연결 리스트(C언어)

✍ 배열 vs 연결리스트

배열과 연결리스트의 장단점을 인지하는 것은 중요하다.

알고리즘 문제에서 시간은 정말 소중하기 때문..^^

문제를 보고 어떤 자료구조를 사용할지에 대한 안목을 기르기 위해서 잘 알아두자.

 

배열

👍 장점

- 임의의 원소에 접근 속도가 빠르고 일정하다.

- 스택이나 큐의 원소를 삽입/삭제하는 등을 수행하고자 하는 작업에 적합하다.

 

👎 단점

- 임의의 원소에 대한 삽입/삭제는 어렵다.

- 크기가 고정되어 있다. (동적 배열로 해결 가능)

- 사용하지 않은 공간에 대한 메모리 낭비가 생긴다.

- 배열 크기가 클 경우 메모리 할당을 받지 못하는 경우가 있다.

 

언제 사용할까

- 데이터 개수가 확실하게 정해져 있을 때

- 데이터의 삽입/삭제가 적을 때

- 검색을 해야할 때

 

연결 리스트

👍 장점

- 삽입/삭제가 간단하다.

- 크기가 가변적이다.

 

👎 단점

- 임의의 원소에 접근이 오래 걸린다.

- 참조 포인터를 위한 메모리 공간이 낭비된다.

 

언제 사용할까

- 크기가 정해져 있지 않을 때

- 삽입/삭제가 자주 일어날 때

- 검색을 자주 하지 않을 때

 

원소	연결 리스트	배열	동적 배열
인덱싱	O(n)	O(1)	O(1)
가장 앞에 삽입/삭제	O(1)	O(n)	O(n)
가장 끝에 삽입/삭제	O(n)	O(1)	배열이 다 찬 경우 : O(n) 배열이 다 차지 않은 경우 : O(1)
중간에 삽입/삭제	O(n)	O(n)	O(n)
낭비되는 공간	O(n)	0	O(n)

 

✍ 자기 참조 구조체

자기 참조 구조체는 자신과 동일한 구조체를 가리킬 수 있는 포인터 변수를 필드 변수로 가지는 구조체이다.

연결 리스트 구조체의 형태를 보면 쉽게 이해할 수 있다.

typedef struct node {
	int data;
	struct node* next;
} NODE;

cf) C는 아직 존재하지 않는 타입에 대한 포인터의 생성을 지원한다.

 

✍ 더블 포인터를 사용하는 이유

본격적으로 단순 연결 리스트를 구현하기 앞서 더블 포인터를 사용하는 이유에 대해 알아보자.

먼저, 단일 연결 리스트에서 삽입/삭제 연산으로 head 포인터의 값을 변화시킬 수 있다.

이때, 호출 함수의 포인터 변수가 참조하는 객체를 피호출 함수에서 바꾸고자 할 경우 이중 포인터를 사용해야 한다.

 

NODE** head 변수가 담고 있는 값은 NODE* head의 주소이다.

NODE* head는 head의 첫번째 주소, 즉 헤드의 주소를 의미한다.

다시 말해, *head는 head의 주소!

 

위의 내용을 잘 이해했는지 확인해보자.

*head == NULL과 head == NULL의 차이는 무엇일까?

 

*head는 head의 첫번째 주소, 즉 헤드의 주소를 의미한다.

헤드가 비었다는 건 *head는 빈 리스트라는 뜻이다.

*head == NULL은 리스트가 비어있으니, 삽입할 경우 head의 주소에 새 노드의 주소를 넣어주면 된다.

head == NULL은 리스트 자체가 존재하지 않는다는 뜻이다.

 

이거를 제대로 인지하지 못하면 뒤에 내용을 이해하기 어려우니 잘 알아두자. 

✍ 단순 연결 리스트 구현

자, 이제 본격적으로 단순 연결 리스트를 구현해볼 것이다.

구현할 때 주의해야 할 점은 *head가 NULL일 때와 그렇지 않을 때 알고리즘 차이를 생각해주어야 한다!

구현할 함수는 아래와 같다.

하나씩 알아보자.

void insert_front(NODE** head, int data); // 맨 앞에 노드 추가
void insert_last(NODE** head, int data); // 맨 뒤에 노드 추가
void print_list(NODE** head); // 연결 리스트 출력
int delete_front(NODE** head); // 맨 앞에 노드 삭제
int delete_(NODE** head, int data); // 해당 data 노드 삭제
int search(NODE** head, int data); // 해당 data가 저장된 노드의 index 출력
void invert(NODE** head); // 역순으로 연산
void sort_insert(NODE** head, int data); // 오름차순으로 노드 추가
NODE* merge(NODE** aHead, NODE** bHead); // 두 연결 리스트 하나로 병합

 

1️⃣ 맨 앞에 노드 추가하기

 

i, ii 경우 모두 *head를 변경시키므로 동일하게 구현해주면 된다.

 

알고리즘

1. NODE 구조체의 포인터인 temp를 동적 할당해준다.

2. 데이터를 temp->data에 삽입한다.

3. temp->next가 *head를 가리키도록 한다. (*head는 head의 첫번째 주소, 즉 헤드의 주소를 의미한다.)

4. *head가 temp를 가리키도록 한다. (head의 첫번째 주소가 temp를 가리킨다.)

 

아래 사진부터 사진의 head는 *head라고 생각하자. 

 

void insert_front(NODE** head, int data) {
	NODE* temp = (NODE*)malloc(sizeof(NODE));
	temp->data = data;
	temp->next = *head;
	*head = temp;
}

 

2️⃣ 맨 뒤에 노드 추가하기

 

i의 경우 *head를 변경시키고, ii의 경우 *head를 변경시키지 않으므로 따로 구현한다.

 

i) *head == NULL일 경우

1. NODE 구조체의 포인터인 temp를 동적 할당해준다.

2. 데이터를 temp->data에 삽입한다.

3. temp->next가 NULL을 가리키도록 한다.

4. *head가 temp를 가리키도록 한다.

 

ii) *head != NULL일 경우

1. NODE 구조체의 포인터인 temp를 동적 할당해준다.

2. 데이터를 temp->data에 삽입한다.

3. temp->next가 NULL을 가리키도록 한다.

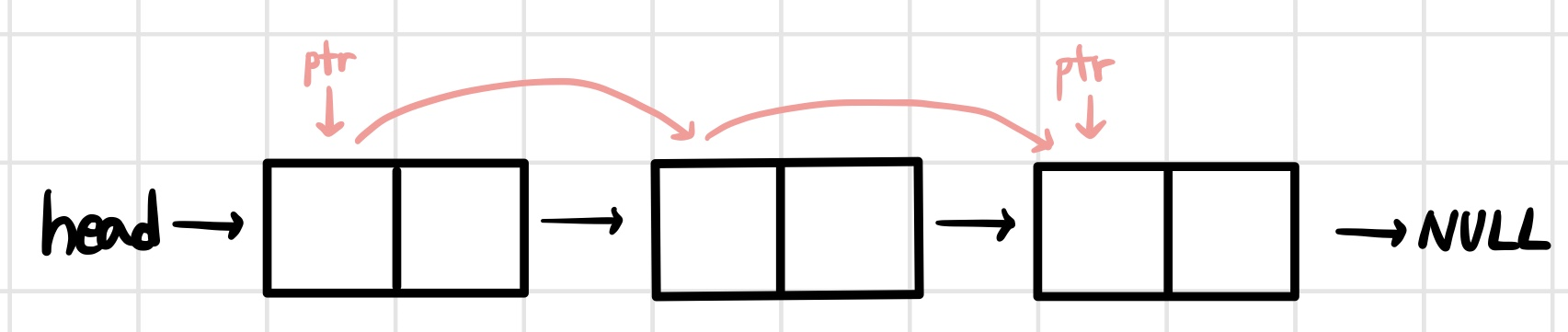
4. ptr 포인터가 *head를 가리키게 하고 ptr->next가 NULL일 때까지 ptr=ptr->next한다. 그리고 ptr->next가 temp를 가리키도록 한다.

void insert_last(NODE** head, int data) {
	NODE* temp = (NODE*)malloc(sizeof(NODE));
	temp->data = data;
	temp->next = NULL;
	NODE* ptr = *head;
	if (*head == NULL) {
		*head = temp;
		return;
	}
	while (ptr->next) ptr = ptr->next;
	ptr->next = temp;
}

 

3️⃣ 연결 리스트 출력하기

 

단순히 탐색하는 연산이므로 *head가 NULL일 경우와 그렇지 않을 경우를 고려하지 않아도 된다.

쉬운 연산이므로 빠르게 넘어가자.

 

알고리즘

1. NODE를 가리키는 ptr 포인터가 *head를 가리키도록 한다.

2. ptr값이 존재할 때까지 ptr->data를 출력해준 뒤, ptr=ptr->next로 옮겨준다.

void print_list(NODE** head) {
	NODE* ptr = *head;
	printf("Head->");
	while (ptr) {
		printf("%d->", ptr->data);
		ptr = ptr->next;
	}
	if (ptr == NULL) {
		printf("NULL");
	}
	printf("\n");
}

 

4️⃣ 맨 앞에 노드 삭제한 후 삭제한 노드의 data 반환하기

i) *head == NULL일 경우

삭제할 노드가 없으므로 -999 값을 반환해줘 오류 처리한다.

 

ii) *head != NULL일 경우

알고리즘

1. NODE를 가리키는 ptr 포인터가 *head를 가리키도록 한다.

2. *head가 *head의 next를 가리키도록 변경한다.

3. 삭제할 노드 ptr를 해제한다.

int delete_front(NODE** head) {
	NODE* ptr = *head;
	if (!ptr) return -999;
	int data = ptr->data;
	*head = ptr->next;
	free(ptr);
	return data;
}

 

5️⃣ 입력 받은 data의  노드를 찾아 삭제하기

 

i) *head == NULL일 경우

삭제할 노드가 없으므로 -999 값을 반환해줘 오류 처리한다.

 

ii) 삭제할 노드가 *head일 경우

알고리즘

1. *head를 *head->next로 변경한다.

 

iii) 이외

알고리즘

1. ptr 값이 존재할 때까지 pre는 ptr의 이전 노드, ptr 노드는 그 다음 노드를 가리키도록 반복한다.

 2. 반복하면서 ptr->data == data일 때 pre->next가 ptr->next를 가리키도록 한다.

int delete_(NODE** head, int data) {
	NODE* ptr = *head;
	NODE* pre = NULL;
	int result = -999;

	for (; ptr; pre = ptr, ptr = ptr->next) {
		if (ptr->data == data) {
			if (ptr == *head) {
				result = ptr->data;
				*head = (*head)->next;
				free(ptr);
				return result;
			}
			else {
				result = ptr->data;
				pre->next = ptr->next;
				free(ptr);
				return result;
			}
		}
	}
	return result;
}

 

6️⃣ 해당 data가 저장된 노드의 index 반환

 

단순히 탐색하는 연산이므로 *head가 NULL일 경우와 그렇지 않을 경우를 고려하지 않아도 된다.

쉬운 연산이므로 빠르게 넘어가자.

int search(NODE** head, int data) {
	int cnt = 0;
	NODE* ptr = *head;
	while (ptr) {
		if (ptr->data == data) return cnt;
		ptr = ptr->next;
		cnt++;
	}
	return -999;
}

 

7️⃣ 역순으로 연산하기

 

역순 알고리즘은 아래 그림을 차례대로 따라가보면 쉽게 이해할 수 있다.

마지막에 *head를 q로 바꾸어 주는 것을 까먹지 않도록 주의해야 한다.

void invert(NODE** head) {
	NODE* p;
	NODE* q;
	NODE* r;

	p = *head;
	q = NULL;
	while (p) {
		r = q;
		q = p;
		p = p->next;
		q->next = r;
	}
	*head = q;
}

 

8️⃣ 오름차순으로 노드 추가하기

i) *head == NULL인 경우

*head가 temp를 가리키도록 한다.

 

ii) 입력받은 데이터가 첫 번째 노드보다 작은 경우

temp가 첫 번째 노드가 되도록 삽입한다.

 

iii) 이외

ptr = ptr->next로 반복하여 변경하면서 탐색한다.

마지막 노드까지 갔을 경우 입력 받은 데이터가 가장 크다는 의미이므로 마지막 노드에 삽입한다.

위의 경우를 제외한 중간 노드에 위치한 경우 아래 그림처럼 처리한다.

void sort_insert(NODE** head, int data) {
	NODE* temp = (NODE*)malloc(sizeof(NODE));
	temp->data = data;
	temp->next = NULL;
	NODE* ptr = *head;
	if (!ptr) {
		*head = temp;
	}
	else if (temp->data <= (ptr->data)) {
		temp->next = *head;
		*head = temp;
	}
	else {
		while (true) {
			if (!(ptr->next)) {
				ptr->next = temp;
				break;
			}
			else if (temp->data < ptr->next->data) {
				temp->next = ptr->next;
				ptr->next = temp;
				break;
			}
			ptr = ptr->next;
		}
	}
}

9️⃣ 두 연결 리스트 하나로 오름차순으로 병합하기

 

i) 둘 중 하나라도 연결리스트가 비었을 경우

*aHead == NULL인 경우, *bHead를 반환한다.

*bHead == NULL인 경우, *aHead를 반환한다.

 

ii) 이외

재귀에 익숙하지 않은 분이라면 약간 어려울 수 있다.

먼저, aHead의 첫번째 노드 data와 bHead의 첫번째 노드 data를 비교한다.

만약 aHead의 첫번째 노드 data가 더 작다면 aHead에 temp에 연결하고 temp->next는 merge(aHead의 두번째 노드, bHead의 첫번째 노드)의 반환값을 가리키게 한다. 이게 재귀적으로 들어가면 마지막엔 aHead 또는 bHead가 NULL이 되어 bHead 또는 aHead가 반환되어 재귀가 끝나게 된다.

 

NODE* merge(NODE** aHead, NODE** bHead) {
	NODE* temp = NULL;

	if (*aHead == NULL) return *bHead;
	else if (*bHead == NULL) return *aHead;

	if ((*aHead)->data < (*bHead)->data) {
		temp = *aHead;
		temp->next = merge(&((*aHead)->next), bHead);
	}
	else {
		temp = *bHead;
		temp->next = merge(aHead, &((*bHead)->next));
	}
	return temp;
}

 

 

전체 코드는 아래 GitHub에 있으니 필요하시다면 참고하세요 !~!

// 추가 예정

 

Reference

C로 쓴 자료구조론, 이석호

https://bluejake.tistory.com/44

 

https://choiiis.github.io/data-structure/basics-of-array-and-list/

 

https://velog.io/@hidaehyunlee/%EC%97%B0%EA%B2%B0-%EB%A6%AC%EC%8A%A4%ED%8A%B8linked-list%EC%97%90%EC%84%9C-%EC%9D%B4%EC%A4%91-%ED%8F%AC%EC%9D%B8%ED%84%B0-%EC%82%AC%EC%9A%A9%ED%95%98%EA%B8%B0

 

저의 이해를 도와준 포스트를 올려주신 분들.. 감사합니다🙇‍♀️